如何等分切分披萨？数学家给你答案！

英国利物浦大学两位数学家设计了一个奇妙的披萨切分流程，该流程不仅仅能够将披萨完美地切分成12等份的小片，而且可以一直切分下去没有极限，甚至可以切分成弯弯曲曲的怪异形状。

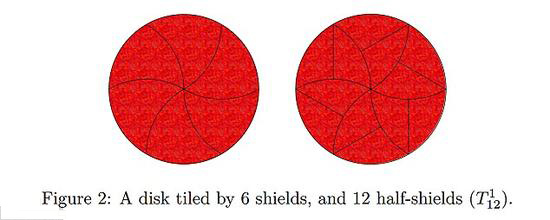
此前相关的研究提出了一种完美的披萨切分法，可将披萨切分成均等的12片，即首先将披萨饼切分成6片弯曲的3边形小片；然后，将这6小片再一分为二，内侧的几片没有硬面皮，外侧的几片则有硬面皮。

据国外媒体报道，全球每年披萨消费量至少50亿份，每秒至少有350小片披萨被吃掉。这些披萨小片究竟是如何被平均切分的呢？如何切分才能实现最完美的均分呢？英国利物浦大学两位数学家通过设计一个切分流程回答了上述问题，该流程不仅仅能够将披萨完美地切分成12等份的小片，而且可以一直切分下去没有极限，甚至可以切分成弯弯曲曲的怪异形状。

此前的相关研究表明，一块披萨饼被切分成12片完全相同的小片是完成有可能的。英国利物浦大学两位数学家乔尔-哈德利和斯蒂芬-沃斯利则更进一步，他们通过实践证明利用他们的方法可以将披萨一直这样均等地切分下去，而且可以切分成弯曲的怪异形状。不过，切分各种形状的小片并非是艺术切分，而是基于几何图形进行切分的。

在此基础上，两位数学家更进一步，将这些曲边形状的小片再切分成更多的面积相等的奇数边小片，然后再按此前的方法将这些小片一分为二。

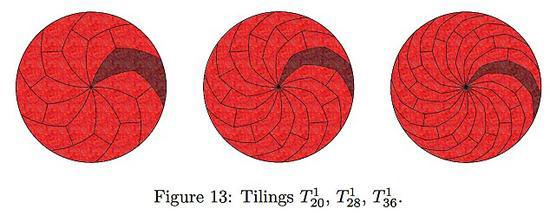
如果继续切下去要，可能还会形成更为怪异的图形。如果继续切下去要，可能还会形成更为怪异的图形。

乔尔-哈德利和斯蒂芬-沃斯利的切分流程是在借鉴此前相关研究基础上进行设计的。此前相关的研究提出了一种完美的披萨切分法，可将披萨切分成均等的12片，即首先将披萨饼切分成6片弯曲的3边形小片；然后，将这6小片再一分为二，内侧的几片没有硬面皮，外侧的几片则有硬面皮。在此基础上，两位数学家更进一步，将这些曲边形状的小片再切分成更多的面积相等的奇数边小片，然后再按此前的方法将这些小片一分为二。

哈德利表示，“从数学角度来讲，这种分法永远没有极限。虽然在切成9边形图案以后，你会发现在实践上很难再进行操作。我不知道这种方法除了用于切披萨外还有何其它的应用，但是这一结果在数学上非常有趣，你可以生成一些非常美丽的图案。”如果继续切下去要，可能还会形成更为怪异的图形。

虽然数学家可以向人们证明理性的完美是可以实现的，但我们知道，从情感层面上，人类很难做到。